As discussed in a previous post [1], distributed control schemes are perceived to be more suitable for future power networks than the centralized counterpart. However, designing such control schemes is more complex than that of the conventional centralized one. Particularly, a distributed control scheme requires communication and cooperation of the controllers, which inherently introduce additional issues if it is not well designed. In this article, we discuss some aspects of communication and cooperation issues and methods that have been proposed to tackle them.
In a distributed control scheme, controllers must be able to exchange information to compute their control inputs. Therefore, a communication network where this process occurs must be available. Furthermore, typically, there are certain communication requirements must be fulfilled to carry out a distributed algorithm. Nevertheless, some issues might arise during the communication process. These include communication failures, delays, and data packet drops [1].
In dealing with some of those problems, the communication network can be regarded as a time-varying network for which some distributed control methods have been proposed. A common approach to develop a distributed algorithm is employing a consensus method. A consensus method allows all controllers to obtain common information across the network even though they are connected through a time-varying and limited communication links. Some distributed control schemes that apply the consensus method, such as formation control and synchronization of coupled oscillators are presented in [2]. Furthermore, some distributed optimization algorithms, e.g., those outlined in [3], also use this concept. In this line of work, we also have proposed a consensus-based information-exchange protocol for distributed model predictive control schemes [4].
A different approach that has been considered is modelling such communication issues as random processes or additional disturbances. In this regard, standard distributed algorithms are extended and studied under this model. For instance, in [5], insufficiency of information from the other controllers is taken into account as an additional disturbance and the control inputs are robustified with respect to that using the so-called tube-based method. Furthermore, the work in [6] shows that a distributed optimization algorithm called the alternating direction method of multipliers (ADMM) might also work over a communication network modelled as a random graph.
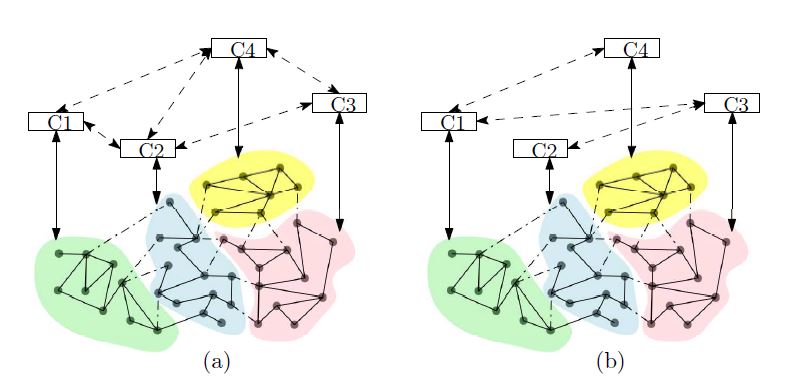
Figure 1: A distributed control scheme with a time-varying communication network.
The second issue that we discuss is related to cooperation of the agents. Any distributed control method requires all controllers to cooperate and comply with the rules/protocols. Therefore, some attention has been given to study potential cases when some agents do not cooperate or comply with the distributed algorithms. For instance, some agents might provide erroneous information to other agents. Another example of malicious actions is implementing control inputs that are different from those, which have been computed by the distributed algorithm.
In the topic of consensus methods, a malicious behaviour, when some agents provide false information to prevent convergence, has been studied and some methods to ensure consensus under this condition have also been proposed. For instance, one can find them in [7,8]. A similar case in a consensus-based distributed control scheme is discussed in [9] where a methodology to detect and deal with this issue is also presented. In the framework of distributed model predictive control, the work in [10] outlines a methodology to deal with non-compliance of some agents. Furthermore, in order to deal with false information problems, a defense mechanism based on the scenario approach is proposed in [11] and a scheme to incentivize truth-telling among agents is proposed in [12]. Our work presented in [?] discusses a non-compliance problem in a distributed economic dispatch scheme of interconnected microgrids. In this work, the malicious actions are modelled as additional disturbances and control inputs are robustified with respect to them. Furthermore, we also propose a methodology to identify the malicious agents and mitigate malicious actions. Specifically, the identification method uses hypothesis testing based on Bayesian inference.
To conclude, some attempts have been initiated to deal with some communication and cooperation issues that might present in a distributed control scheme. Given the relevance to the control of future power networks, improving the resiliency is an important task in designing a distributed control scheme.
References


