Synchronization is a fascinating and fundamental physical phenomenon found in many different systems with vastly different sizes. It can be found in mechanical, biological or chemical systems as well as human behavior or human made structures, for example in power systems. The first observation and description of synchronization was made by scientist Christiaan Huygens in the 17th century. Huygens observed that two pendulum clocks, connected by a wooden beam, would start to swing simultaneously. After a while, their movement was so in phase that the sound of each clock was heard at the same time. Furthermore, even after disturbing the synchronized motion, the system would return to synchronized behavior after a short time. This behavior would today be called stable synchronized motion.
A very illustrative example of synchronization are metronomes, as illustrated in the following video:
While synchronization was discovered a long time ago and serious scientific interest can be dated back to the work of van-der-Pol in the 1920s, a full understanding of synchronization is still not possible. Synchronization is a non-linear effect [2], which makes all analysis difficult. Many effects can only be explained by computer simulations or analyzed in simplified systems.
- Conditions for synchronization
Synchronization usually appears in system with the following properties:
- Autonomous oscillatory behavior of independent units
- A coupling mechanism between the units
In the example of the pendulum clocks, each clock is the independent unit which oscillates (swings) on its own. The wooden beam acts as the coupling mechanism. In general, each oscillator may be a bit different from each other. To achieve synchronization, the coupling must overcome the dissimilarity of the individual oscillators. The following applet shows the behavior of the famous Kuramoto model and can be used to get some intuition for the coupling strength. Each dot represents the phase of an oscillator, which rotates with its own frequency. The slider can be used to adjust the coupling strength between the oscillators. For small (or zero) couplings, each oscillator will rotate independently. Increasing the coupling strength above a certain threshold will result in synchronized, unified rotation of all oscillators. If the coupling strength is decreased, the oscillators will return to rotate in their own, natural frequency.
2.1. Networks
In the classical Kuramoto model, each oscillator is connected with each other oscillator. An interesting example is the clapping of an audience in a theater. Each member of the audience is an oscillator and claps at an own frequency. At the same time, each member hears the clapping of all other members and will (maybe just slightly) adjust his own clapping frequency.
Sometimes, this will result in synchronized clapping, as observed in the following video:
In fact, some features usually found in synchronized system can be identified in clapping audiences [1].
In many man-made systems, as well as some systems in nature, only certain oscillators are directly coupled. For example, the intestinal smooth muscle of mammals oscillate with an intrinsic frequency and are electrically coupled to only neighboring cells. The synchronization of these cells will trigger the contraction of the muscle.
Which oscillators are coupled in a large system can be studied by the connections network and its graph structure. Each connection in the network corresponds to a real-world coupling between the two oscillators.
The structure of the underlying network will have a great influence in the behavior of the systems and especially its synchronization. Consider the two example networks with N = 4 oscillators:
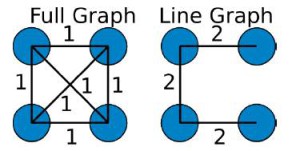
In the system called full graph, all oscillators are coupled (with coupling weight 1) with each other. In system called line graph, there is only a line connecting all oscillators. Even if we increase the coupling strength for the line graph at each connection, the full graph may be easier to synchronize.
To illustrate this behavior, the following plots show the behavior of a full and line graph system with N = 40 oscillators. The coupling strength at each connection is 1 for the full graph and 40 for the line graph system:

Here, an order parameter of 1 corresponds to total synchronization. It is clear that the full graph is synchronized, while the line graph is not. In general, a densely connected network will synchronize more easily.
- Synchronization in power systems
For a stable operation, the power system has to be synchronized. In a very simplified view, the power system consists of coupled generators (which convert mechanical power to electrical power) and electrical machines (which convert electrical to mechanical power). From a mechanical point of view, these devices correspond to rotating masses. Each mass will rotate with an individual frequency, which will depend on the in- and output of the device.
In the power grid, the electrical frequency, which is linked to the rotating frequency of the rotating masses, should be identical. The individual devices are coupled via the transmission network and the structure of the network will influence the stability. This coupling may result in spontaneous frequency synchronization. While the full power system is heavily controlled and regulated, the property of natural autonomous synchronization is very important for the stability of the power system.
3.1. Challenges in the study of synchronization
The autonomous synchronization of the power system is a key to stable operation. As discussed previously, stable synchronization in complex networks depends on the shape of the network. With the inclusion of renewable energies, storage units active demands and other advanced components in the power grid, the complexity of the network will increase (see also the blog article from Nicolas Retière [3]). Many technical advancements towards smart grids, like energy storage (with the problem of low inertia) or demand forecast and management are made, the natural stability of the power system has to be considered. Challenges include:
- How does the change in network topology influence the synchronization and stability?
- Are the models used to study synchronization suitable? How do the effects of synchronization depend on the models?
- Is synchronization possible in heavily stressed grid?
- How do strongly fluctuating energy sources, like renewable energies and adaptive load behavior influence the stability of the synchronization in the power grid
In general, the study of synchronization in power system is still an important field of research with many new interesting challenges. The connection to other scientific fields in which synchronization can be observed makes it even more important and interesting to follow.
For more insight into synchronization, the book [2] and the following TED talk by Steven Strogatz are recommended:
References
[1] Z. Néda, E. Ravasz, T. Vicsek, Y. Brechet, and A. L. Barabási. Physics of the rhythmic applause. Phys. Rev. E, 61(6):6987–6992, June 2000. [2] Arkady Pikovsky, Michael Rosenblum, and Jürgen Kurths. Synchronization: a universal concept in nonlinear sciences, volume 12. Cambridge university press, 2003. [3] Nicolas Retière. Complexity paves the path to smart electrical systems, INCITE blog post April 2017.




