Monte Carlo simulation and Multistage stochastic programming approaches for the day-ahead scheduling of local energy systems
The implementation of microgrids is considered useful to enable the increasing integration of decentralized energy producers. However, the volatility of renewable energy generation and demand behaviour is one of the biggest challenges for the operation of local energy systems, with an optimal fulfilment of the energy demand.
This post focuses on an electric local energy system, e.g. the power system of an industrial site or of a residential neighbourhood, including a photovoltaic (PV) unit capable to provide a significant part of the local energy consumption. The system is also equipped with an energy storage unit in order to fully exploit the available renewable energy source even with limited capability of the external utility network to which the system is connected Fig 1. This scenario is realistic in many present situations, as shown in [1], [2] and references therein.
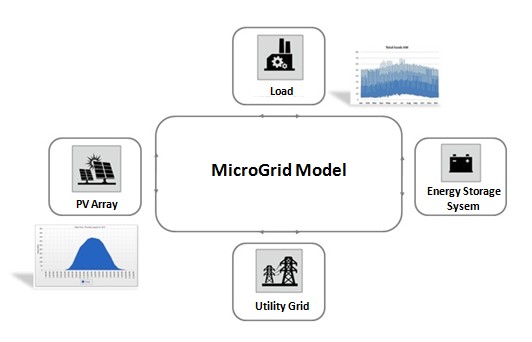
Fig. 1 - The structure of the considered local energy system
We aim at providing a brief overview at several optimization approaches to minimize the energy cost within the microgrid incorporating the influence of short-term uncertainty.
Modelling under the assumption of perfect information
The first approach is to solve the optimization problem assuming that all the information is certain, i.e. by the implementation of a deterministic model. In such a model, it is assumed that the future information relevant to the production from renewable resources and the load consumption in the system are known [3].
A typical aim of the Energy Management System (EMS) is the minimization of the production costs associate with PV, storage units and the power exchange with the external network to feed the internal load during time horizon.
The use of a cost minimization objective function needs the knowledge of the values of the various prices. An alternative objective could be the minimization of the power exchange with the external power distribution network.
The implemented model determines the optimum day-ahead scheduling for the battery operation. Fig. 2a shows the deterministic results obtained by using a cost minimization objective with the energy consumption and the PV generation profiles shown in Fig. 2b. Two profiles for the state of charge of the battery are shown one obtained by using two different models for the battery: the kinetic model and the simple model given by the energy equilibrium.
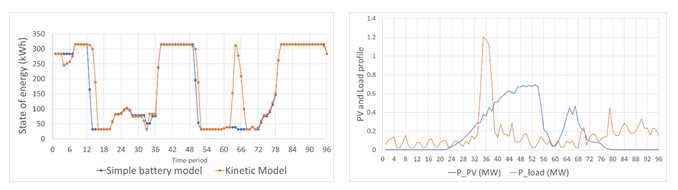
Fig. 2 - a) State of charge of the battery calculated by using the kinetic model and the simple model, and b) profiles of the load and PV production
Approaches to deal with uncertainties
Since the forecasts of both renewable sources production and load consumption are affected by significant uncertainties, stochastic linear programming or Monte Carlo simulation are typical adopted (e.g., [4],[5]). We compare these different approaches as illustrated in Fig. 3.
The uncertainties are described through stochastic processes, conveniently characterized using scenarios. For this purpose, we adopt a scenario-generation procedure that incorporates the correlated behaviour of the prediction and its hourly profile by using the properties of a Markov-Process approach [6].
The Monte Carlo Simulation (MCS) method is one of the most widely used in decision-making considering uncertainty. Samples of the stochastic process (called scenarios) are considered as a set of input data. The deterministic solution is obtained for each scenario. Then the mean value solution of set of results is calculated.
The use of multistage stochastic programming requires, in general, the application of a scenario-reduction technique in order to limit the computational effort [3].
This work includes the implementation of different scenario-reduction techniques, namely a heuristic based approach and k-means clustering able to reduce the computational effort while keeping as much as possible the information contained in the set of the original scenarios.
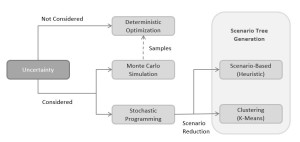
Fig. 3 - Diagram of the implemented approaches
Intraday decision function
Given the solution of the day-ahead scheduling provided by the multi-stage stochastic programming, a decision-making function is needed to choose the consecutive decisions at each stage. In order to accomplish this decision process, in the actual operation during the day, the decision-making function is based on the calculation of the Euclidean distance between the actual operating conditions, defined by the PV production and the load consumption in the hours of the last stage, and the scenarios of the tree. The decision to be implemented is the one relevant to the scenario closest to the actual operating conditions.
Therefore, the decision-making function accomplishes the two following tasks:
- calculated the Euclidean distances;
- decides the set point values of the battery power output for each time interval of the following stage.
Fig. 4 shows the generated scenario tree and, in red, the successive decision steps provided by the decision-making function for a test scenario.
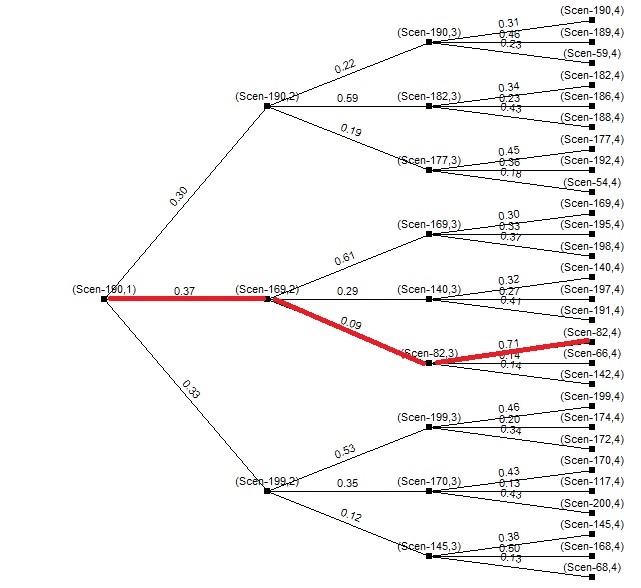
Fig. 4 - Scenario tree and, in red, an example of the solution provided by the decision-making function
Example of the results
As an example of the results, Fig. 5 shows the comparison between the values of the objective function by using the average decision provided by the Monte Carlo simulation method and the decision obtained by the stochastic optimization approach, for several different scenarios. As expected, Fig. 5 shows a reduction in the energy costs over the local system that represents the so-called of the value of the stochastic solution [3].
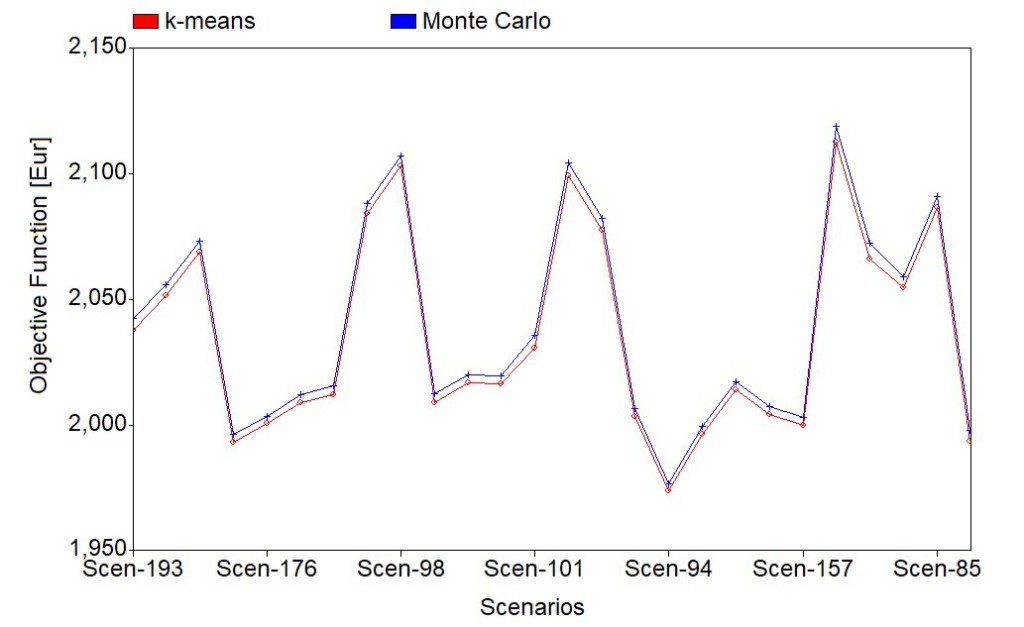
Fig. 5 - Comparison between the values of the objective function by the MCS and by the stochastic optimization approach based on k-means clustering technique
The comparison with the results obtained by Monte Carlo simulations provides useful insights on the influence of the uncertainties in the day ahead scheduling of the local energy system.
References
[1] G. Graditi, M. G. Ippolito, E. Telaretti, and G. Zizzo, “Technical and economical assessment of distributed electrochemical storages for load shifting applications: An Italian case study,” Renew. Sustain. Energy Rev., vol. 57, pp. 515–523, 2016. [2] R. van Leeuwen, J. B. de Wit, and G. J. M. Smit, “Energy scheduling model to optimize transition routes towards 100% renewable urban districts,” Int. J. Sustain. Energy Plan. Manag., vol. 13, pp. 19–46, 2017. [3] A. J. Conejo, M. Carrión, and J. M. Morales, Decision Making Under Uncertainty in Electricity Markets. Springer, 2010. [4] S. S. Reddy, V. Sandeep, and C.-M. Jung, “Review of stochastic optimization methods for smart grid,” Front. Energy, vol. 11, no. 2, pp. 197–209, 2017. [5] G. C. Lazaroiu, V. Dumbrava, G. Balaban, M. Longo, and D. Zaninelli, “Stochastic optimization of microgrids with renewable and storage energy systems,” EEEIC 2016 - Int. Conf. Environ. Electr. Eng., 2016. [6] G. J. Osório, J. M. Lujano-Rojas, J. C. O. Matias, and J. P. S. Catalão, “A new scenario generation-based method to solve the unit commitment problem with high penetration of renewable energies,” Int. J. Electr. Power Energy Syst., vol. 64, pp. 1063–1072, 2015.
